Feladat:
- Ábrázoljon egy origó középpontú kört!
- GY: Ábrázoljon egy kört, amelynek a középpontja megadható!
- GY: Ábrázoljon egy ellipszist!
Előkészítés
Mindhárom feladatra igaz, hogy az x és az y nem fejezhető ki egymásból, egy x értékhez több y érték is rendelhető és fordítva. A megoldáshoz először le kell vezetnünk a képleteket, amiket majd az Excel táblázatba be tudunk írni. A levezetést az origó középpontú körre mutatjuk be.
Az origó középpontú kör egyenlete:
R² = x² + y²,
ahol R a kör sugara. Megfigyelhetjük, hogy a kör paraméterezhető a középponti φ szöggel és pont origótól vett r távolságával. Azaz polárkoordináta-rendszerben is felírhatjuk:
r(φ) = R.
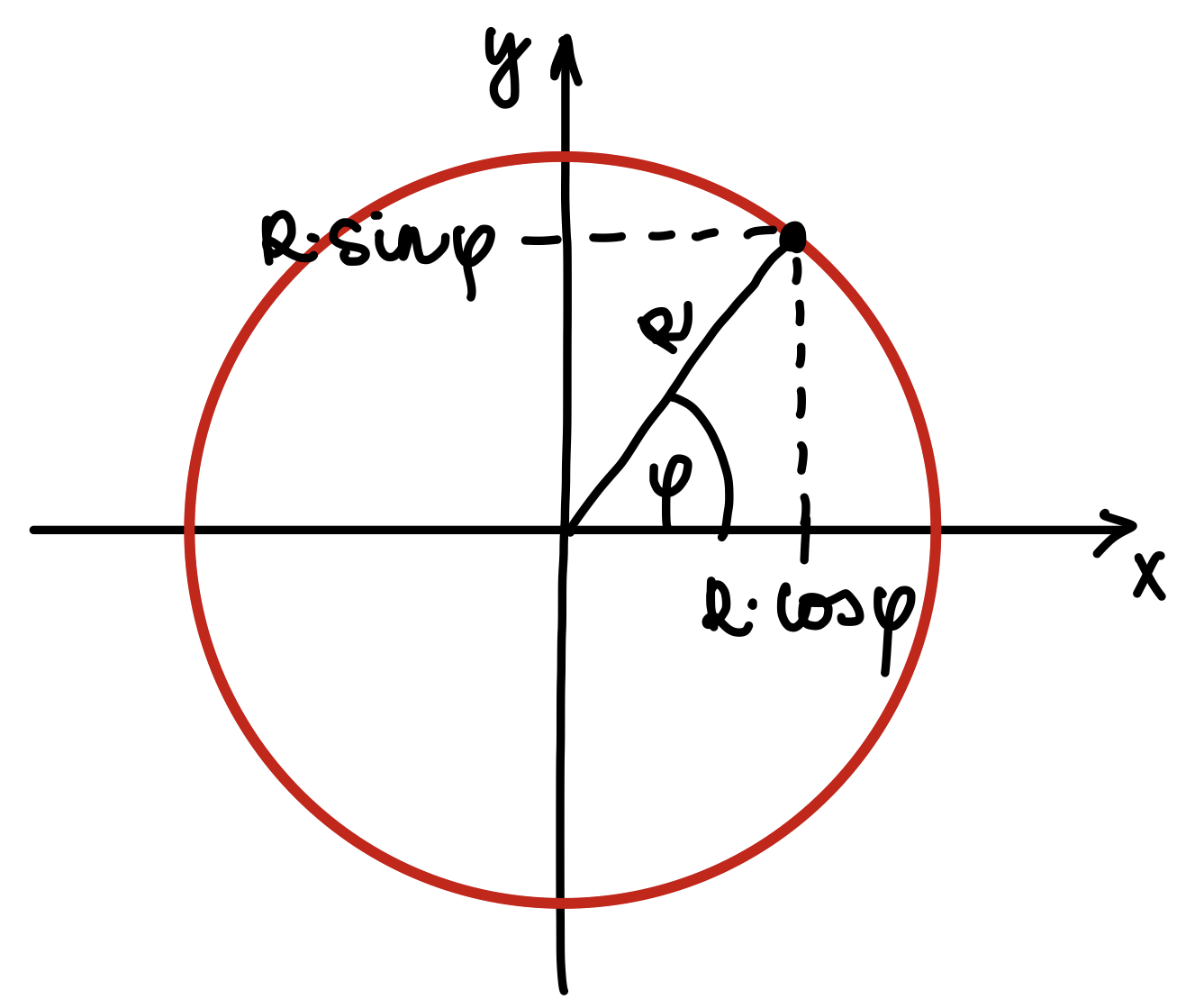
A φ függvényében már kifejezhető az x és az y:
x(φ) = r(φ) ⋅ cos(φ),
y(φ) = r(φ) ⋅ sin(φ), 0 ≤ φ ≤ 2π
Mivel most speciálisan minden pont ugyanolyan távol van az origótól, ezért az r(φ) konstans, helyére beírhatjuk az R értéket.
TIPP: A fenti összefüggések nem csak a körre, hanem minden más olyan függvényre is alkalmazhatók, amelyeket hasonló módon az origótól vett távolsággal és egy szöggel paraméterezünk. Lásd: Cardioid görbe parametrikus felírása.
A feladat megoldásának lépései:
- φ értékek felvétele egyenletesen 0 és 2π között
- r értékek felvétele minden φ-hez (most konstans R)
- x és y számítása r és φ-ből
1. Feladat: origó középpontú kör
A megoldásban fel kell vennünk az R paraméternek egy cellát, majd pedig három oszlopra lesz szükségünk: φ, x, y. El kell döntenünk, hogy hány pontot szeretnénk ábrázolni, azaz hány darab φ értéket veszünk fel. Legyen ez a szám most n = 20.
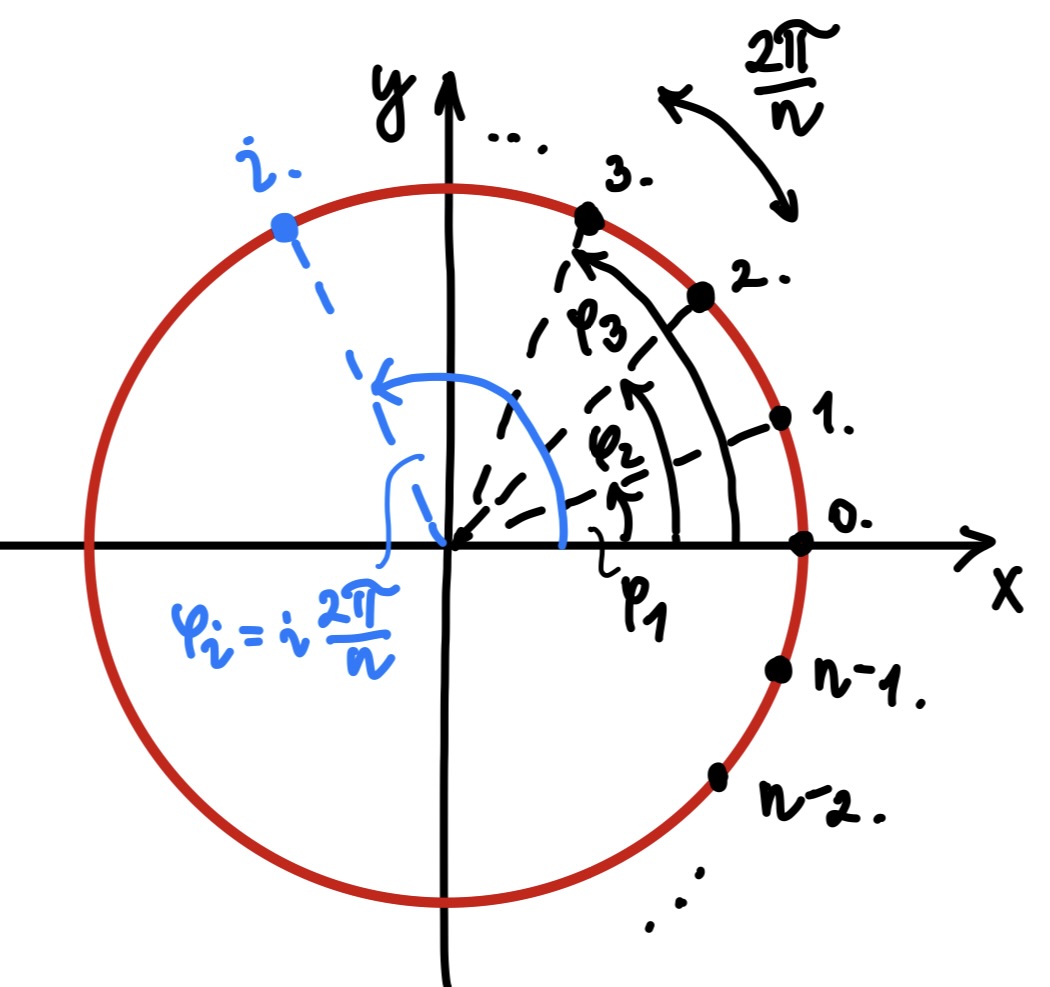
Hogyan tudunk felvenni egyenletesen 0 és 2π közötti értékeket?
Tegyük fel, hogy n részre szeretnénk osztani a kört. Egy megoldási lehetőség, ha minden pontot beszámozunk 0-tól (n-1)-ig (így osztjuk a kört pontosan n részre). Ezután minden ponthoz tartozó szöget a sorszámának és n-nek a segítségével fejezünk ki. Egy osztásköz 2π/n szöget jelent, így az i-edik ponthoz az i⋅2π/n szög fog tartozni.
- A B2 cellába írjuk be, hogy "R = ", a C2 cellába pedig írjunk be egy tetszőleges számot (pl. 2). Nevezzük el a C2 cellát rr-nek.
- A B4, C4, D4, E4 cellákba kerülnek a fejlécek: i, phi, x, y.
- A B5 cellába írjuk be, hogy 0, a B6 cellába pedig, hogy 1. Ezután jelöljük ki a két cellát, majd a jobb alsó sarokban lévő négyzetre kattintva lefelé húzással másoljuk a képletet addig, míg az n-1-ig el nem jutunk (19). Az egyszerűség kedvéért nevezzük el az egész B oszlopot i-nek: kattintsunk a B oszlop fejlécére - ezzel a teljes oszlopot kijelöljük -, majd írjuk át a nevét.
- A C5 cellába írjuk be a phi képletét, majd másoljuk lefelé, végül nevezzük el az oszlopot phi-nek:
= @i*2*PI()/20
TIPP: Miért szükséges a két zárójel a PI()-ben? Mert minden Excel függvényre úgy kell hivatkozni, hogy a függvény neve után két zárójel következik. Ez egy speciális beépített Excel függvény, amelynek nincsenek bemeneti paraméterei, ezért nem írunk semmit a zárójelekbe.
TIPP: Miért kell @ az i elé? Az újabb Excelekben megjelent dinamikus képletek óta a @ jellel tudjuk jelezni, ha a tartománynak csak az adott sorban lévő elemére van szükségünk. Most a C5 cellában a B5 cella értékére szeretnénk hivatkozni, ezért kell a @.
- A D5 cellába írjuk be az x képletét:
= rr*COS(@phi) - A E5 cellába írjuk be az y képletét:
= rr*SIN(@phi) - Másoljuk mindkét képletet lefelé duplakattintással.
Már csak az ábrázolás van hátra. Az x-y koordinátarendszerben szeretnénk ábrázolni a pontokat, mindegyiknek kiszámoltuk az x és az y koordinátáit.
- Jelöljük ki az x és az y oszlopokat a fejlécükkel együtt.
- Az Insert menüben válasszuk a diagramok közül a "Scatter with straight lines and markers" opciót.
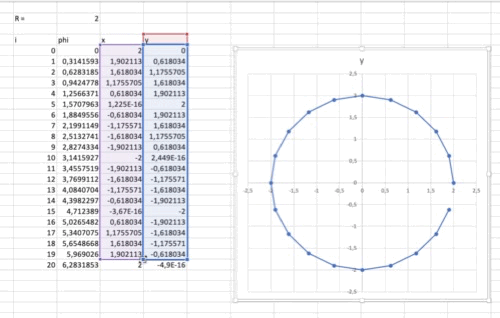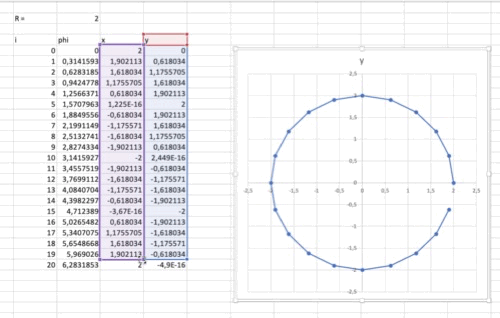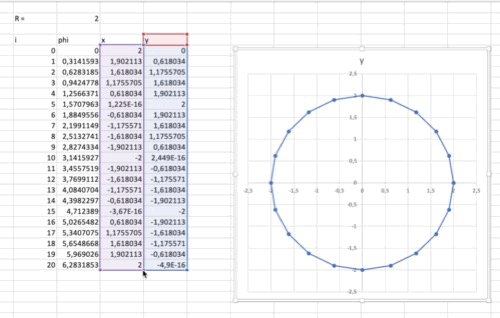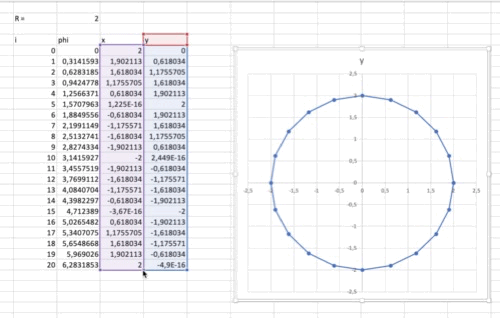
A diagrammal több probléma is van: nem kör alakú és nem zárt. Méretezéssel tudjuk elérni, hogy arányhelyes legyen a diagram. Addig változtassuk a magasságot/szélességet, míg a rácsozás négyzetessé nem válik. Ekkor az x és y osztásközök azonos nagyságúak. A másik probléma megoldható, ha beszúrunk egy plusz sort a táblázatba, azaz felveszünk egy n indexű pontot. Ehhez ugyanaz a szög fog tartozni, mint a 0. ponthoz, így bezárul a kör.
- Méretezéssel tegyük arányhelyessé a diagramot, hogy valóban kör alakú legyen a függvény.
- Az i oszlop aljára, a B25 cellába írjuk be, hogy 20.
- Másoljuk a többi oszlop képleteit, hogy a 25. sorban is megkapjuk az x,y értékeket.
- Formázzuk a diagramot, állítsunk be feliratokat, növeljük meg a betűméretet, hogy jól olvasható legyen.
2. feladat: tetszőleges középpontú kör (gyakorló feladat)
A feladat megoldásához újabb levezetésre van szükség, mivel eddig az origó középpontú kör képleteit vezettük le. A kör általános egyenlete:
R² = (x-xo)² + (y-yo)²,
ahol (xo,yo) a kör középpontjának koordinátái.
Ha a kör minden pontját eltoljuk a középpontjának a koordinátáival, akkor újból egy origó középpontú kört kapunk és a korábbi összefüggések igazak lesznek:
x(φ) - xo = r(φ) ⋅ cos(φ),
y(φ) - yo = r(φ) ⋅ sin(φ), 0 ≤ φ ≤ 2π
Innen, és felhasználva, hogy a sugár továbbra is konstans:
x(φ) = R ⋅ cos(φ) + xo,
y(φ) = R ⋅ sin(φ) + yo, 0 ≤ φ ≤ 2π
A feladat megoldása az előzőhöz hasonlóan történik, a különbség, hogy itt az egy helyett 3 paraméter van: R, xo, yo.
TIPP: Ha ezt a feladatot ugyanabban az Excel dokumentumban szeretnénk megoldani, mint a másikat, de egy másik fülön, akkor a sugár értékét tartozó cellát nem nevezhetjük ismét rr-nek, mert az a név már foglalt. R2-nek sem nevezhetjük, mert az is foglalt, az R2 cellára mutat. Használhatunk név helyett abszolút hivatkozást, vagy nevezhetjük "radius"-nak. Ugyanígy az i és phi oszlopoknak is új nevet kell kitalálnunk, vagy relatív hivatkozással hivatkozhatunk rájuk.
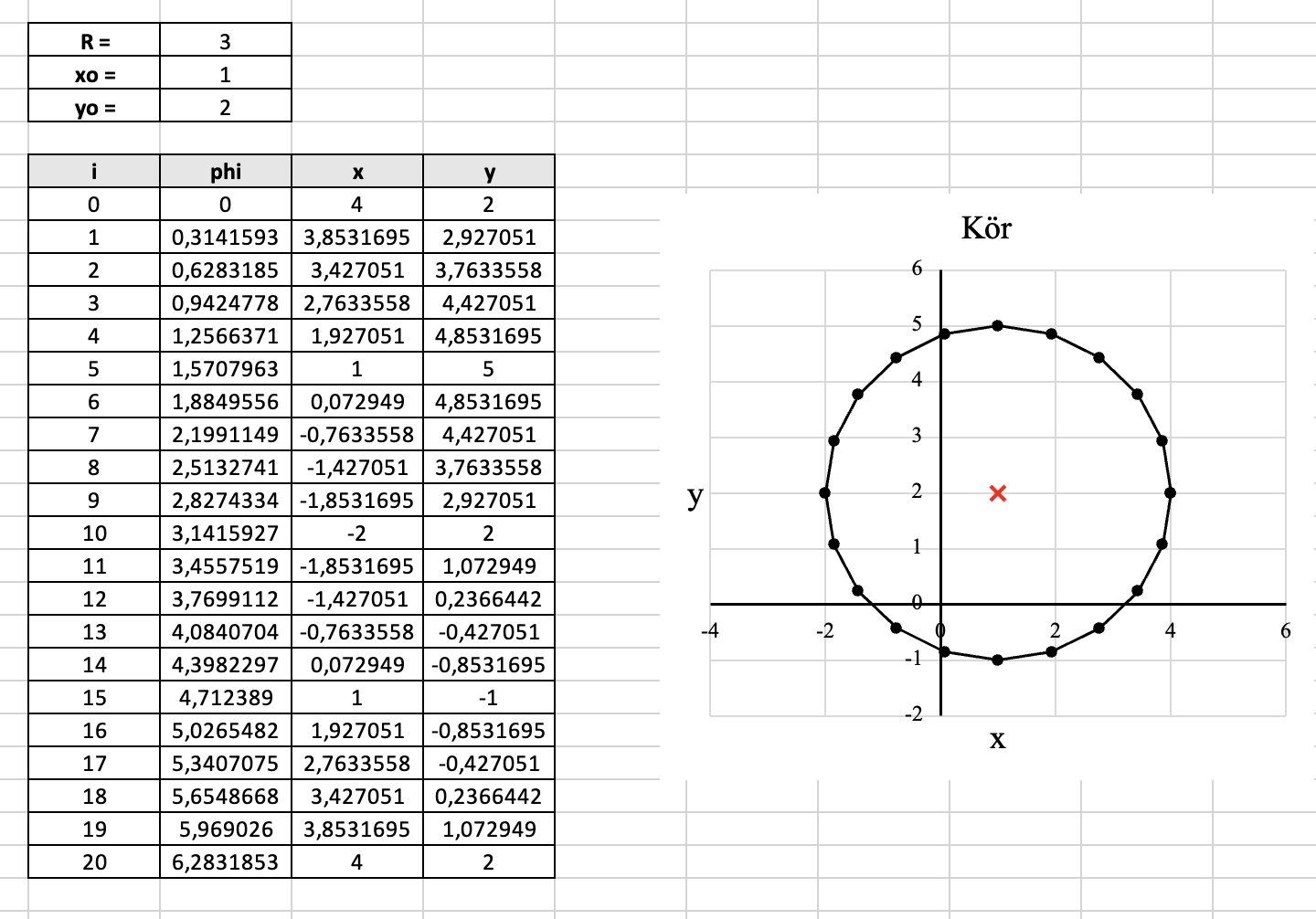
Ellenőrzésképpen ábrázolhatjuk a kör középpontját is.
- Kattintsunk jobb gombbal a diagram egy üres részére, majd a Select data menüben adjunk hozzá egy újabb adatsort a diagramhoz.
- Az x értékekhez hivatkozzunk arra a cellára, amelybe az xo értéket írtuk és ugyanígy az y értékekhez az yo-t tartalmazó cellára kell hivatkozni.
- Formázzuk a diagramot, állítsunk be feliratokat, növeljük meg a betűméretet, hogy jól olvasható legyen.
3. feladat: ellipszis (gyakorló feladat)
A feladat megoldásához szükség van az ellipszis képletére. A képlet internetes kereséssel fellelhető. A lépések a fentiekhez hasonlóak.