Feladat:
Előkészítés
Amennyiben a függvényt kicsi egyenes szakaszokkal közelítjük, úgy az ívhossz közelíthető a kis egyenes szakaszok hosszának összegével. Minden kis szakasz hossza Pitagorasz-tétellel számítható.
Minden két szomszédos pont közötti szakasz alatti terület egy olyan trapéz, amelynek az oldalai ismertek. Ezeknek a trapézoknak kell kiszámolni és összegezni a területét, hogy megkapjuk a terület közelítő értékét.
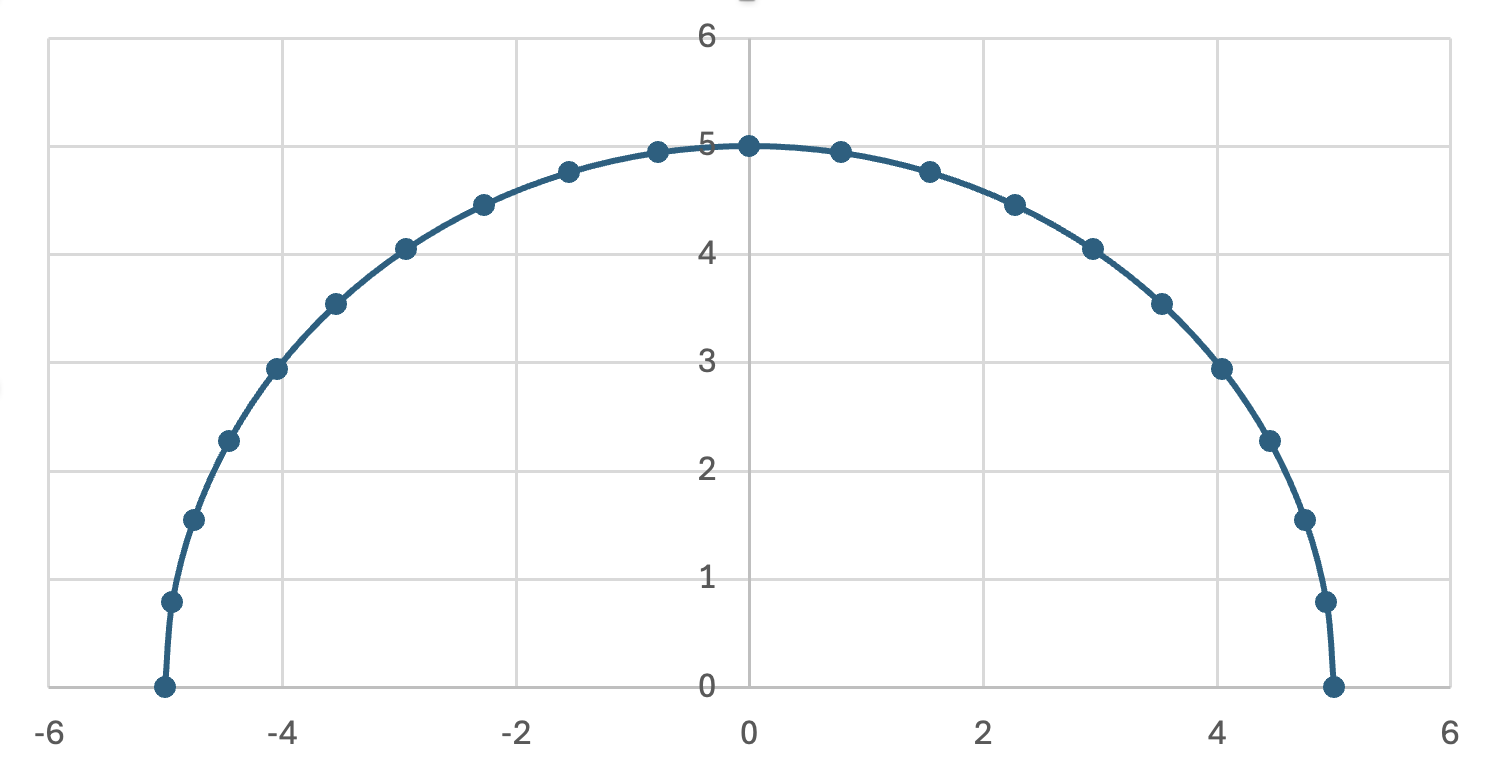
1. Feladat: félkör
Feladat: Ábrázoljon egy félkört, majd számítsa ki az ívhosszát és a területét! Vesse össze az eredményét az analitikus megoldással! Számítsa ki a közelítés hibája.
A megoldásban fel kell vennünk az R paraméternek és a félkörön felvett pontok számának egy-egy cellát, majd pedig az alábbi oszlopokra lesz szükségünk: i, φ, x, y.
A φ értékét most 0 és π között kell egyenletesen felvenni, mivel csak egy félkört ábrázolunk.
Analitikus megoldások: a félkör területe: T = R²π/2, a kerülete: K = Rπ.
A közelítés hibáját megkapjuk, ha a számított és az analitikus értékek különbségét kiszámoljuk. Használjuk az ABS() függvényt a hiba abszolútértékének kiszámításához!
Megoldását összevetheti a megoldókulccsal.

2. feladat: Cardioid görbe (gyakorló feladat)
Feladat: Ábrázoljon egy cardioid görbét, számítsa ki az ívhosszát és a területét! A területet vesse össze az analitikus megoldással!
A Cardioid görbe implicit függvény, ráadásul konkáv is. Amennyiben helyesen írjuk fel a terület képletét, úgy a konvex részeken pozitív, a konkáv részeken negatív lesz a terület értéke, így a szokásos módon számolható az összterület.
A terület analitikus értéke: 3πa²/2.
Megoldását összevetheti a megoldókulccsal.